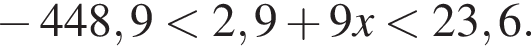Укажите номера уравнений, которые не имеют действительных корней.
1) 
2) 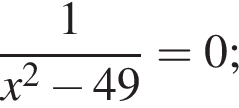
3) 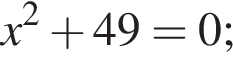
4) 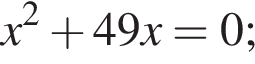
5) 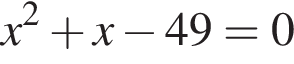
Укажите номера уравнений, которые не имеют действительных корней.
1) 
2) 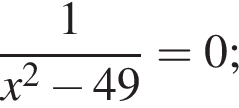
3) 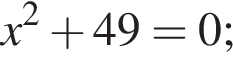
4) 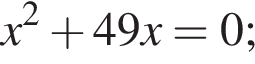
5) 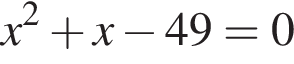
Найдите произведение координат точки пересечения прямых 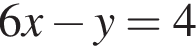 и
и 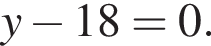
Даны квадратные уравнения:
Укажите уравнение, которое не имеет корней.
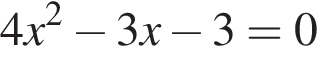
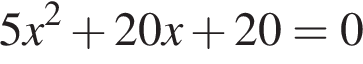
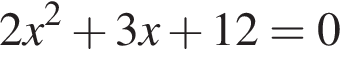
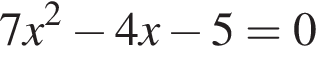
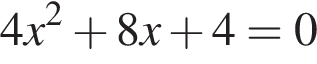
Укажите номер квадратного уравнения, произведение действительных корней которого равно 5.


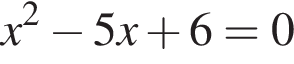
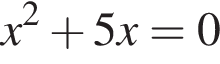

Если 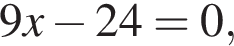 то
то 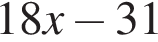 равно:
равно:
Укажите номер квадратного уравнения, корнями которого являются числа x1 − 1, x2 − 1, где x1, x2 — корни квадратного уравнения 3x2 − 5x − 6 = 0.
1) x2 + x − 6 = 0;
2) 3x2 − 11x + 8 = 0;
3) 3x2 − x − 8 = 0;
4) 3x2 + 11x + 8 = 0;
5) 3x2 + x − 8 = 0.
Определите, на сколько неизвестное слагаемое меньше суммы, если известно, что x + 20 = 80.
Даны пары значений переменных x и y: 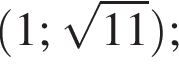
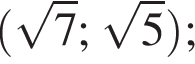

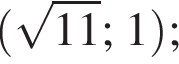
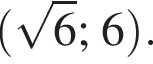 Укажите пару, которая НЕ является решением уравнения
Укажите пару, которая НЕ является решением уравнения 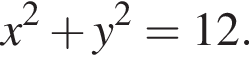
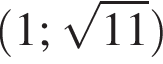

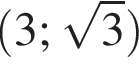
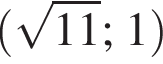
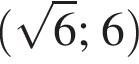
Корень уравнения 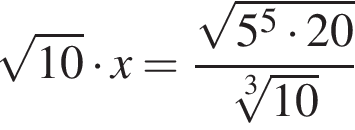 равен:
равен:
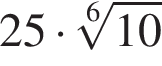
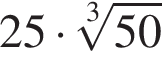
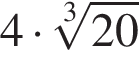
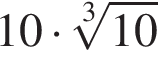
Найдите сумму наименьшего и наибольшего целых решений двойного неравенства 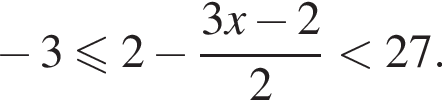
Если 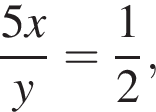 то значение выражения
то значение выражения 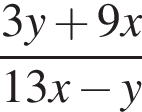 равно:
равно:
Найдите модуль разности наибольшего и наименьшего корней уравнения 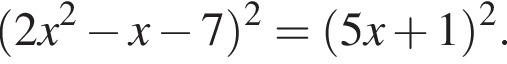
Определите, на сколько неизвестное уменьшаемое больше вычитаемого, если известно, что 
Пусть x1 и x2 — корни уравнения 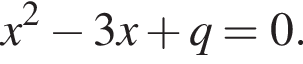 Найдите число q, при котором выполняется равенство
Найдите число q, при котором выполняется равенство 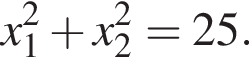
Даны пары значений переменных x и y: (3; 9); (−15; 3); (0; 12); (14; −2); (6; 6). Укажите пару, которая НЕ является решением уравнения x + y = 12.
Сумма всех натуральных решений неравенства 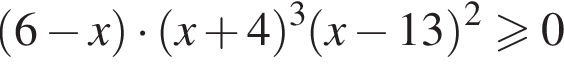 равна:
равна:
Среди чисел −7; −8; −5; −6; −9 укажите то, которое является решением неравенства 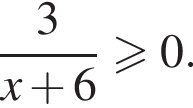
Среди чисел −1; −2; −3; −5; −10 укажите то, которое является решением неравенства 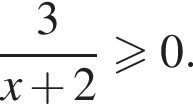
Для неравенства (8 − x)(x + 3) ≥ 0 укажите номера верных утверждений.
1) Число 0 не является решением неравенства;
2) неравенство равносильно неравенству 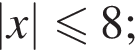
3) количество всех целых решений неравенства равно 12;
4) неравенство верно при x ∈ [−2; 3];
5) решением неравенства является промежуток [−8; 3].
Укажите номера пар неравенств, которые являются равносильными.
1) (x − 14)2 < 0 и x − x2 − 14 ≥ 0;
2) x2 − 169 > 0 и |x| < 13;
3) x2 + x − 30 < 0 и (x − 5)(x + 6) < 0;
4) x2 ≥ 31 и 
5) 5x2 < 9x и 5x < 9.
Найдите сумму всех целых решений неравенства 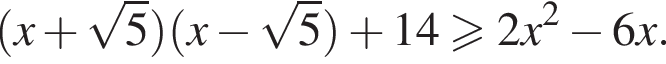
Укажите номера верных неравенств, если известно, что 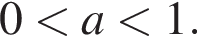

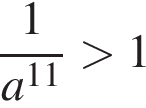
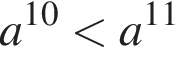
Укажите номера верных неравенств, если известно, что 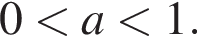
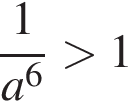
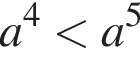

Решением неравенства
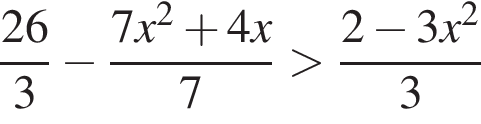
является промежуток:
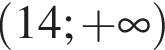 ;
;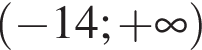 ;
;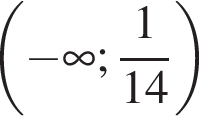 ;
;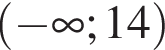 ;
;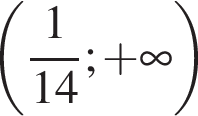 .
.Найдите сумму целых решений неравенства 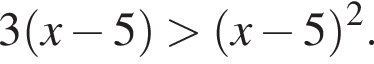
Найдите сумму наименьшего и наибольшего целых решений двойного неравенства